√ダウンロード 多項式の��開 係数 699031-多項式の展�� 係数

式と証明 ３次式の展開について 日々是鍛錬 ひびこれたんれん

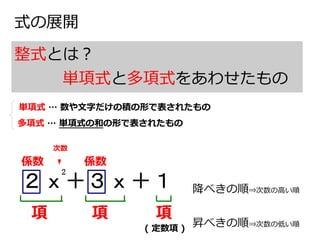
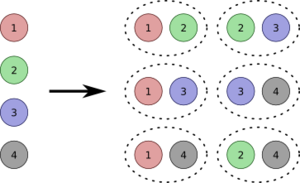
 （1）問題概要 (abc)ⁿなど3項以上の展開式のある項の係数を答える問題。 （2）ポイント 多項展開式の一般項 を使いましょう。 また、 rの値が見てすぐに分からないときは、rを含んだ方程式を立てます。 その際、指数法則を正しく使うことに注意しましょう。 多項式の次数 次数が最も大きい項は （次数 ） → 次数は ちなみに、式全体の次数 に注目して、多項式を「 次式」と呼ぶこともあります。 多項式 は「二次式」ですね。 ② 係数 係数 文字を含む項の 数字部分 。 多項式 において、文字を含む項は「 」と「 」で、それぞれの係数（つまり数字部分）は と です。 ③ 定数項 定数項 文字が含まれない、 数字のみからなる項 。 多項式 におい

多項式の展開 係数

多項式の展開 係数- 実関数F(x)チェビシェフ多項式の係数をFFTを使って求められるらしいのですがどうやって求めたらいいのかわかりません。 F(x)=1/2*c0*T0(x)\sum cn*Tn(x)) と展開したと 多項式の基本6｜3次以上の展開と因数分解の公式の総まとめ 1 22/3/15 多項式 前々回の記事で説明したように，たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は，いったん解を求めることによって因数分解できるのでした． では，3次式では因数分解するための公式や方法はあるのでしょうか？ 3次の場合にも2次式の場合と同じく，3次

3

 多項展開式の係数の問題について質問です (12a3b)^7 a^2b^3 という問題の答えがどうしても合いません 答えは になるようなのですが、何度やってもになってしまいます 立式は 7！/2！3！×2^2×(3)^3 で合っているでしょうか？ 回答お願いします展開公式を丸ごと覚えるのではなく，導けるようにしましょう。 19 19 19 も同様に式の対称性と多項定理から一瞬で導けます。 このように対称式の展開は「対称性，多項定理，係数の和」に注目 して瞬時に行えるようになっておくのが理想です。 エルミート多項式は 母関数をテーラー展開 (マクローリン展開)した場合の展開係数 として知られている エルミート多項式の母関数のテーラー展開係数による定義は, である exp ( x )は簡単に計算できて, であるので, x = t ^22 ξt としてやれば, が得られる ここで次のような数列を考えてやる t の次数が n の時の展開係数が Hn ( ξ )であったので, i j = n ,0≤ j ≤ i を満たす負でない整数 (

いるエルミート多項式による一般フーリエ級数展開の 具体例に触発され，多項式に対して展開係数を具体的 に求める問題を考えた． 21 (2x)n のエルミート多項式による展開 定理2 0 以上の任意の整数n に対して次式が成り立 つ．(6 () 式) (2x)n = n ∑2 rImport sympy sympyvar('x') f = 2*x**3 x 5 fcoeff(x, 3) # => 2;この式を展開したとき、xyの係数は4ですね。 ですからこれは簡単にわかると思います。 のように展開が簡単にいく場合は問題がないですが、 のように展開が面倒くさいときに、二項定理を使って係数を求めることができるのです。 それでは試しに、 を展開したとき、 の係数を求めてみましょう。

多項式の展開 係数のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
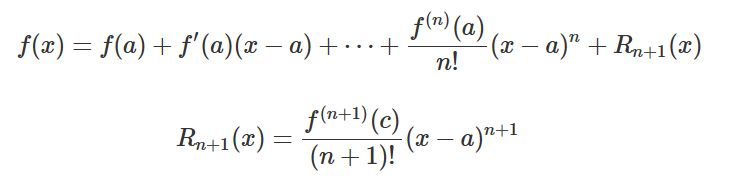乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	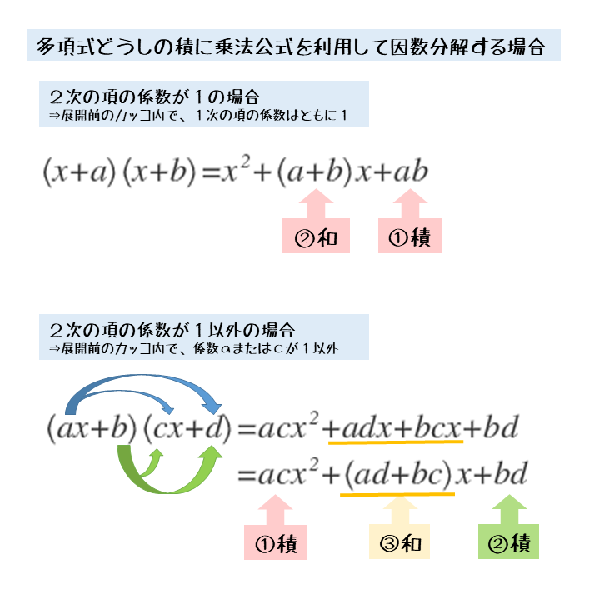乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	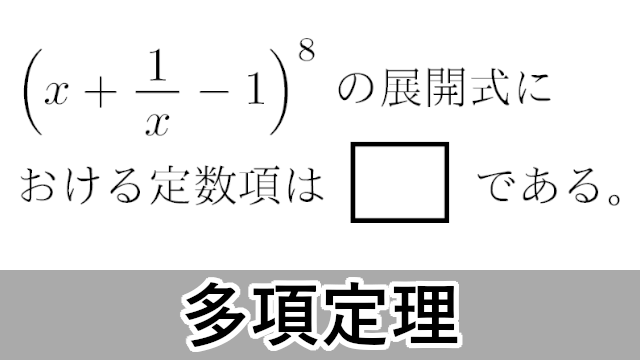乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	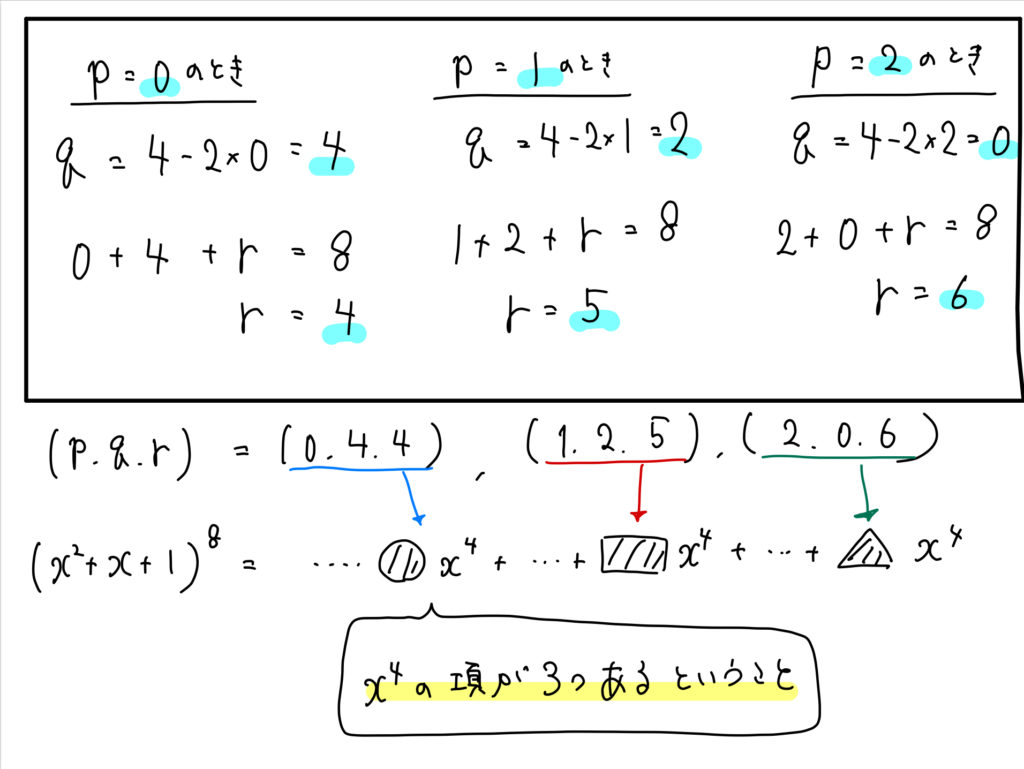乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	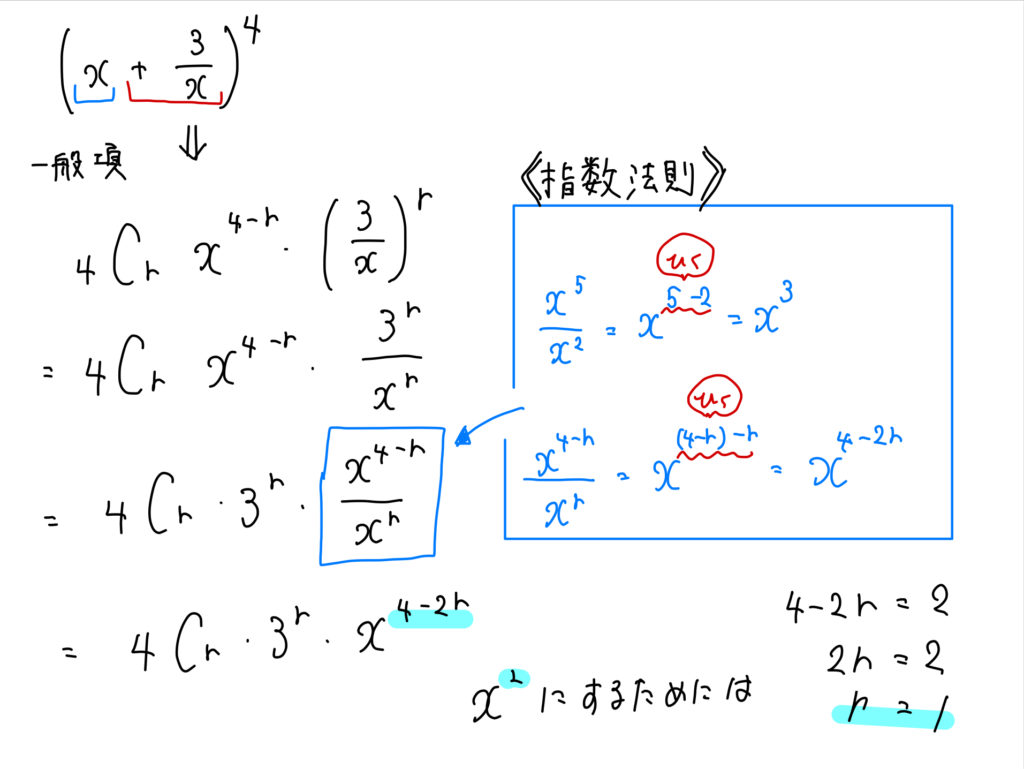乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	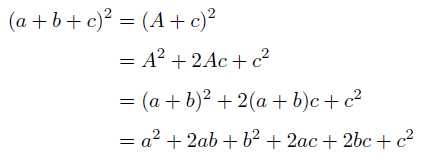乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
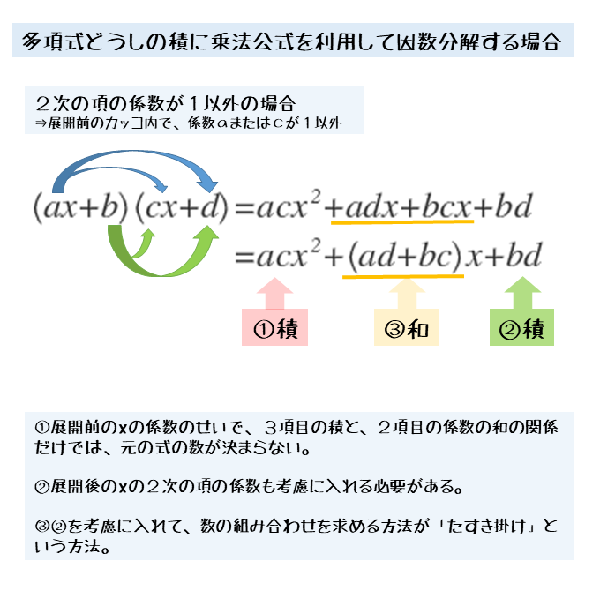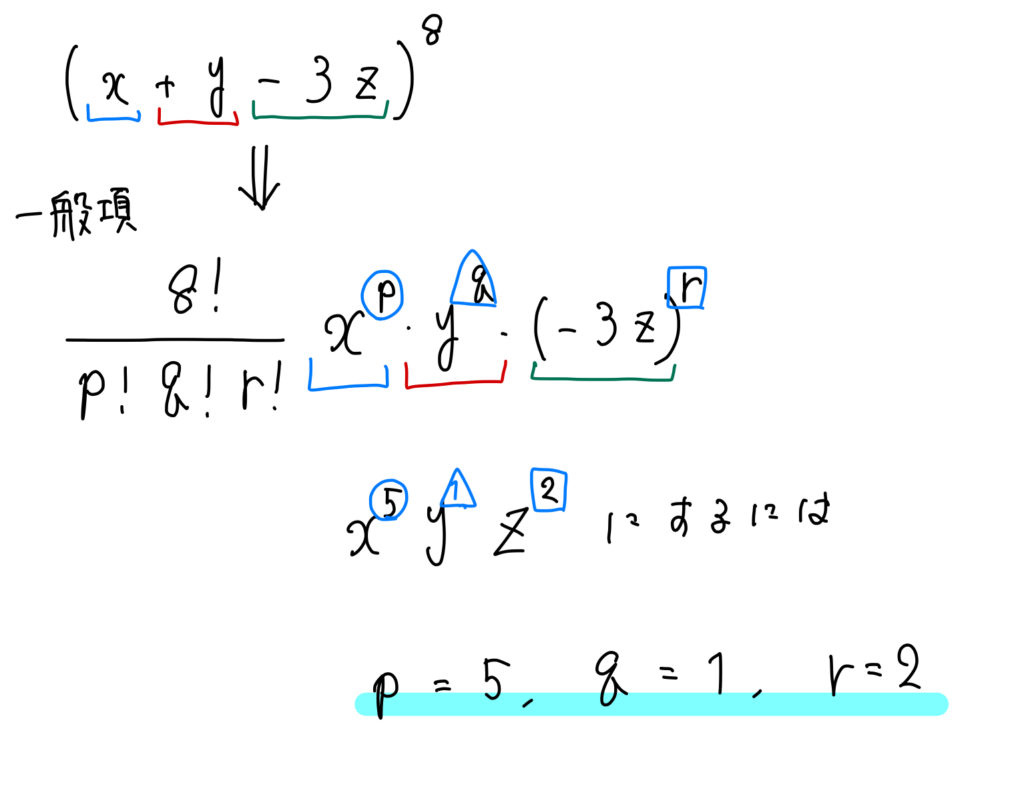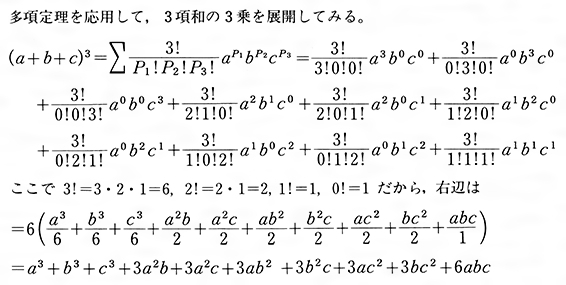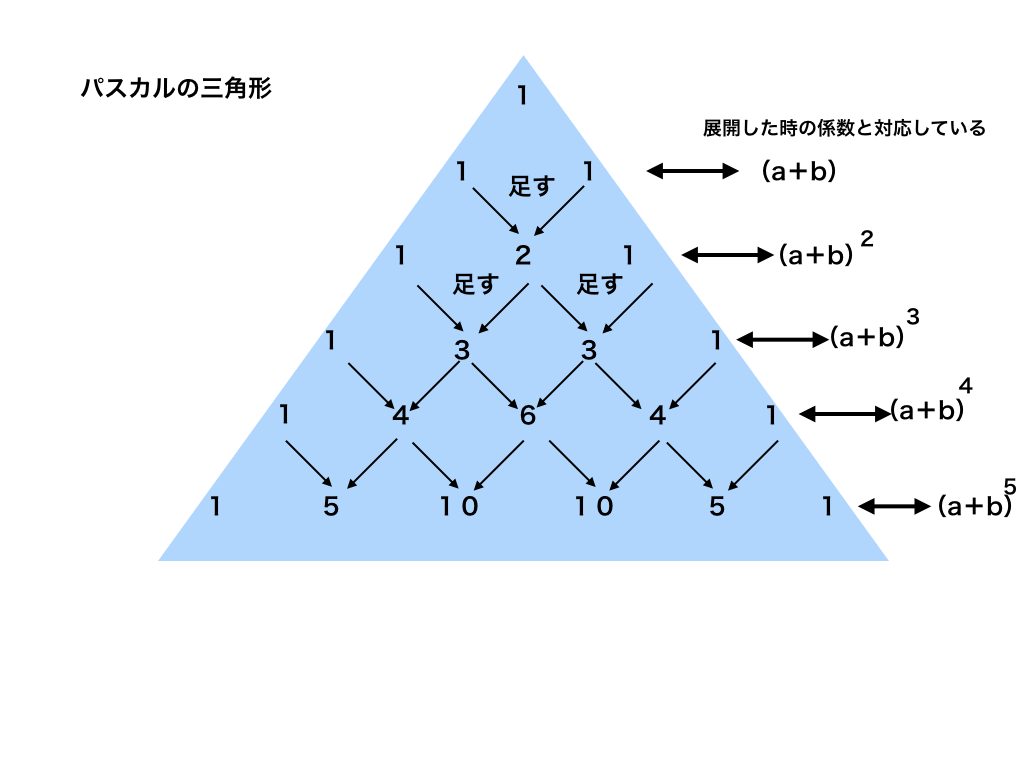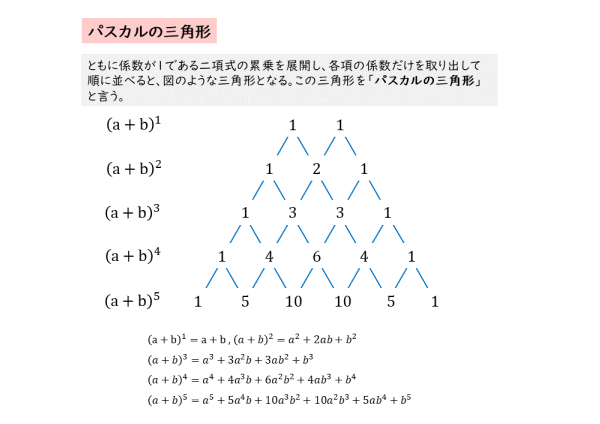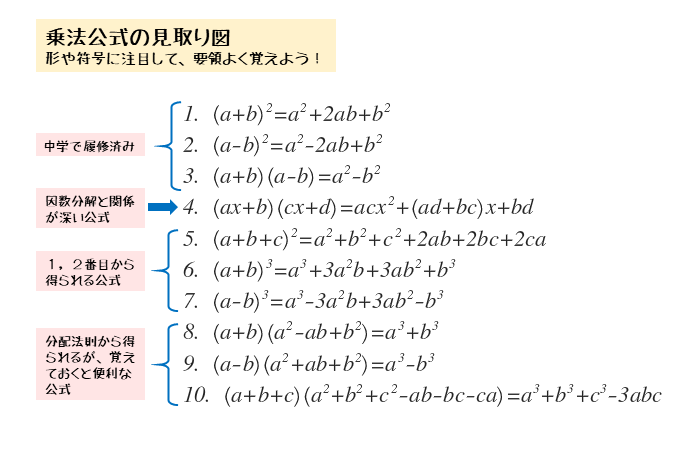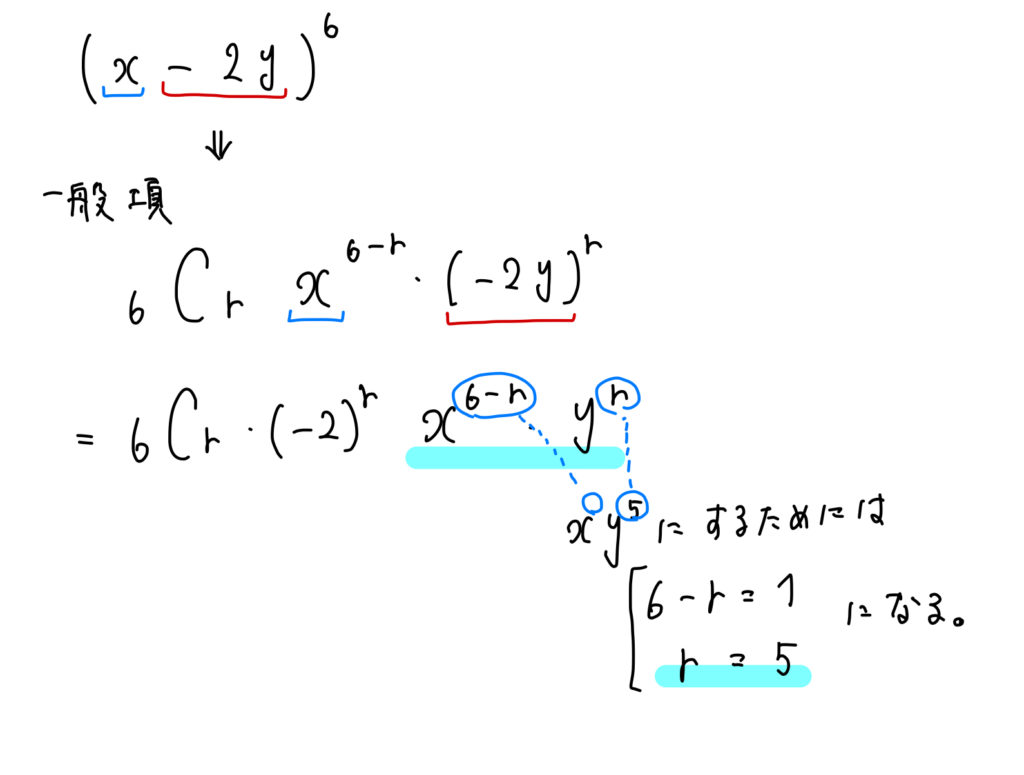乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
乗法公式 多項式の展開公式 の覚え方と使い方 数学fun	乗法公式 多項式の展開公式 の覚え方と使い方 数学fun

 多項定理について 多項定理 は、二項定理における二項式を多項式に対して一般化したものです。 多項式であることから、複数の項をもつ式を展開します。 多項式を展開することを考えると、かなり不安になるかもしれませんが、そこまで心配することはありません。 具体例 この公式を用いて「 (x 1)(x 2) ( x 1) ( x 2) 」を展開すると以下の通り。 展開した式の x x の係数は「左辺の定数項の和」なので「1」と「2」の和の『3』、定数項は「左辺の定数項の積」となるので「1」と「2」の積の『2』になります。 「 (x 2)(x −3) = x2 − x− 6 ( x 2) ( x − 3) = x 2 − x − 6 」を展開すると以下の通り。 展開した式の x x の係数は「左辺の

Incoming Term: 多項式の展開 係数,