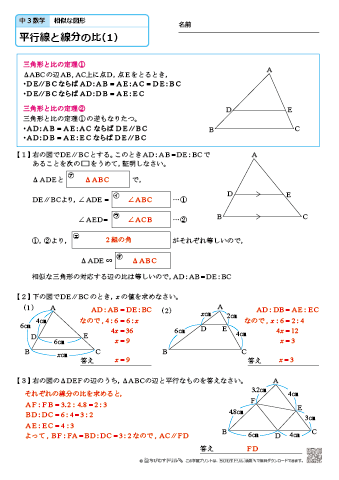
応用問題が出されたときに 対応しきれない部分もあるので できるだけ、比を辿っていく方法で覚えておいて欲しいです。 裏ワザ公式は、答えがあっているかの確認などで 利用してもらえれば効果バツグンなはずです(^^) 平行線と線分の比似 10 「平行線と比」の定理を利用して,線分 課題把握,解決の見通しや確認を行う。 の長さなどを求めることができるようにす る。 の 応 11 三角形の2辺を等しい比に分ける2点を結 べば,その線分は残りの辺に平行となること 用 を考えさせる。平行線と比1(小さい辺:大きい辺) 平行線と比2(上:下) 平行線と比3(平行→線分比) 右の図のように, ab=10cm, ad=6cm, a 6 cm d zabc<90°
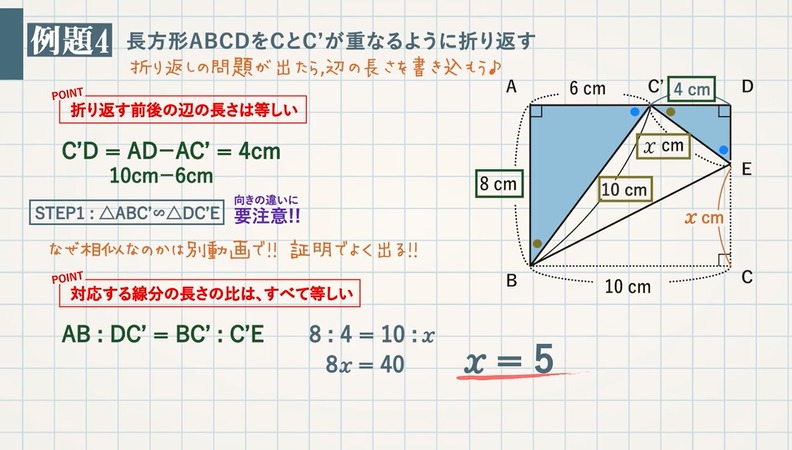
平行線と線分の比 辺の長さを求める応用問題4選 教遊者
平行線と線分の比 台形 応用
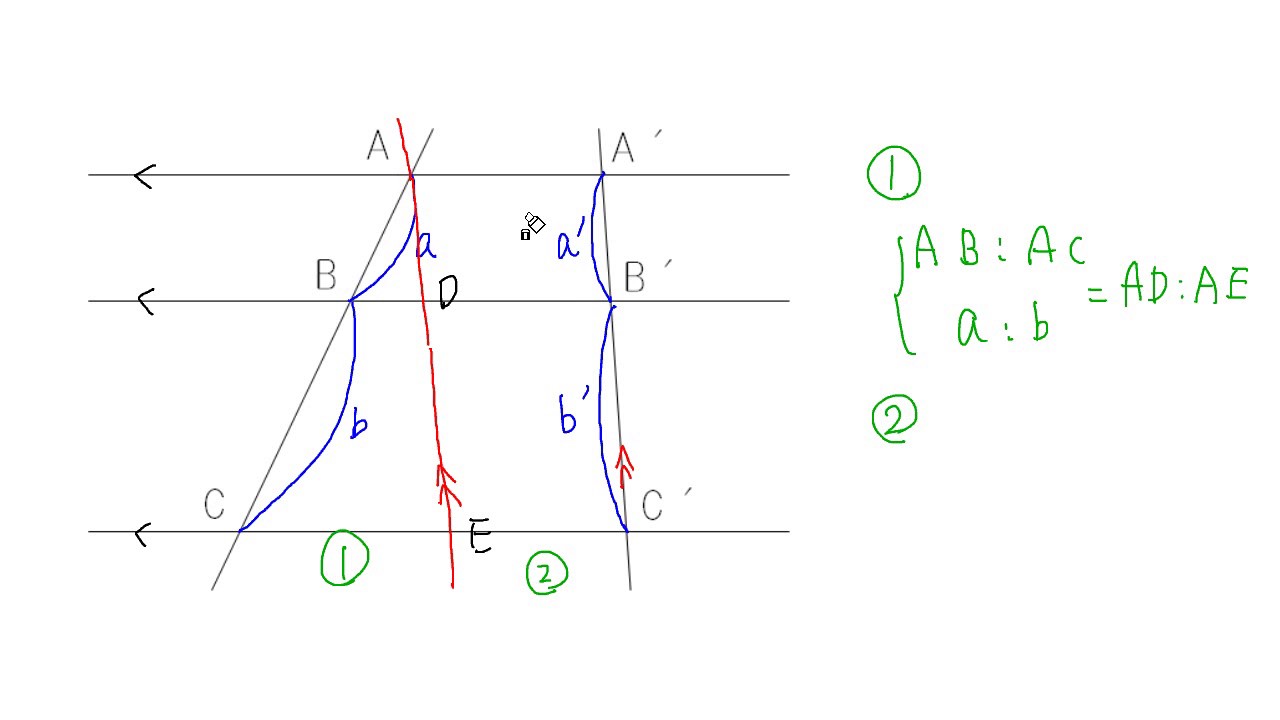
平行線と線分の比 台形 応用-線分比・面積比の応用問題です。長方形の内部の三角形の相似がテーマになります。「線分比を求める問題」の「長方形01・02」「長方形と連比01・02」の逆算・発展です。 応用問題112 01 小6以上。線分比・面積比の応用問題です。直線 t を平行移動させた t' も、 当然 a':b' ですね!




中学3年の数学 動画 平行線と線分の比 基本編の問題 19ch
平行線の線分比の問題の解法 平行線の線分比の性質を使った問題です。 図形を見てどことどこが相似になりそうかわかるようになると良いですね。 記事を読む平行線が作る2つの三角形は相似になります。 ※相似の問題の解法の応用問題をご参照ください 相似から線分比を使って求めます。 (1)の図形は度々定期試験等で出題されます。平行線と線分の比 1 課 題 平行線の性質をもとにして、生徒たちが調べたこ とをそれぞれ生徒に説明(証明)させるという課題 学習である。生徒一人一人が自分で課題を設定し、 自分の力で証明していくのであるから、学習内容は 生徒によって異なる。
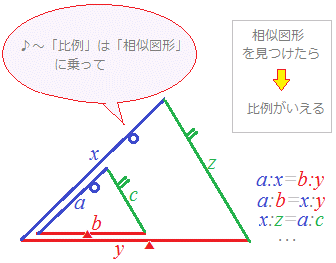
である平行四辺形abcd において, zdab f 10 cm の二等分線と辺 bcのcの方へ延長した直線との交点をe とする。・中3数学 相似と線分比1(平行四辺形) 636 ・平行線と線分の比_06 平行線と比の発展問題 その2 1327 ・線分の比と面積比中学3年数学 1228 ・高校入試 補助線を引いて解く面積比 17 ・数学中353 相似と面積②(応用編) 1357 ・相似の面積比高校入試三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。 ルールは 2つの図形のパターン について
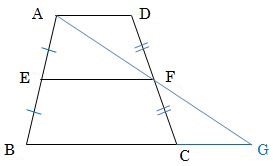
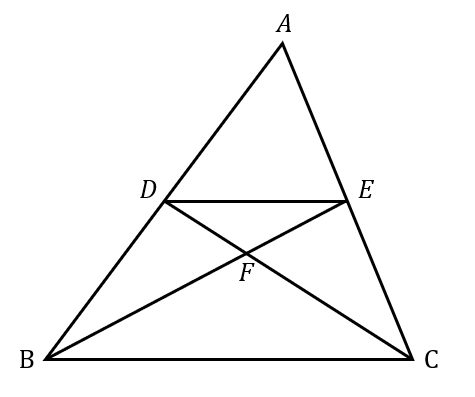
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru数学24章図形の調べ方「平行線と角」<準備問題> 中学数学 平面図形と平行線の性質 平行線と角 ドリるーむ 中2数学直線と角の関係(対頂角・同位角・錯角)について解説! 錯角・同位線分 ec と対角線 bd との交点を f とし,点 f を通って辺 bc に平行な直線と辺 ab との交点を g とします。 このとき,線分 EG の長さを求めなさい。 (埼玉県17年入試問題)




中3数学 相似の平行線と線分の比のポイントと定期テスト対策問題
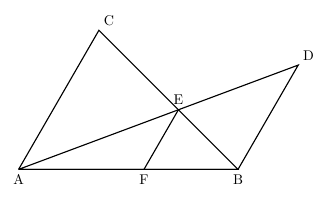



平行線の線分比の問題の解法 夢を叶える塾
ゆうき先生 3分でわかる!平行線と線分の比の2つの証明 平行線と線分の比を証明しなきゃいけない?? ある日、数学が苦手なかなちゃんは、平行線と線分の比 下の図で、直線 \(l,m,n\) が平行ならば、線分の長さの比について以下のことが成りたつ。 \(abbc = deef\) これはなぜ成り立つのか。 下の図のように、\(df\) と平行な線分平行線と線分の比について調べることができる。 相似の考え方を活用することができる。 立体の相似の意味と,相似な図形の相似比や面積比,体積比の関係を理解し,それを利用できる。 4 単元の指導
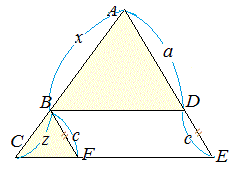



平行線と線分の比



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
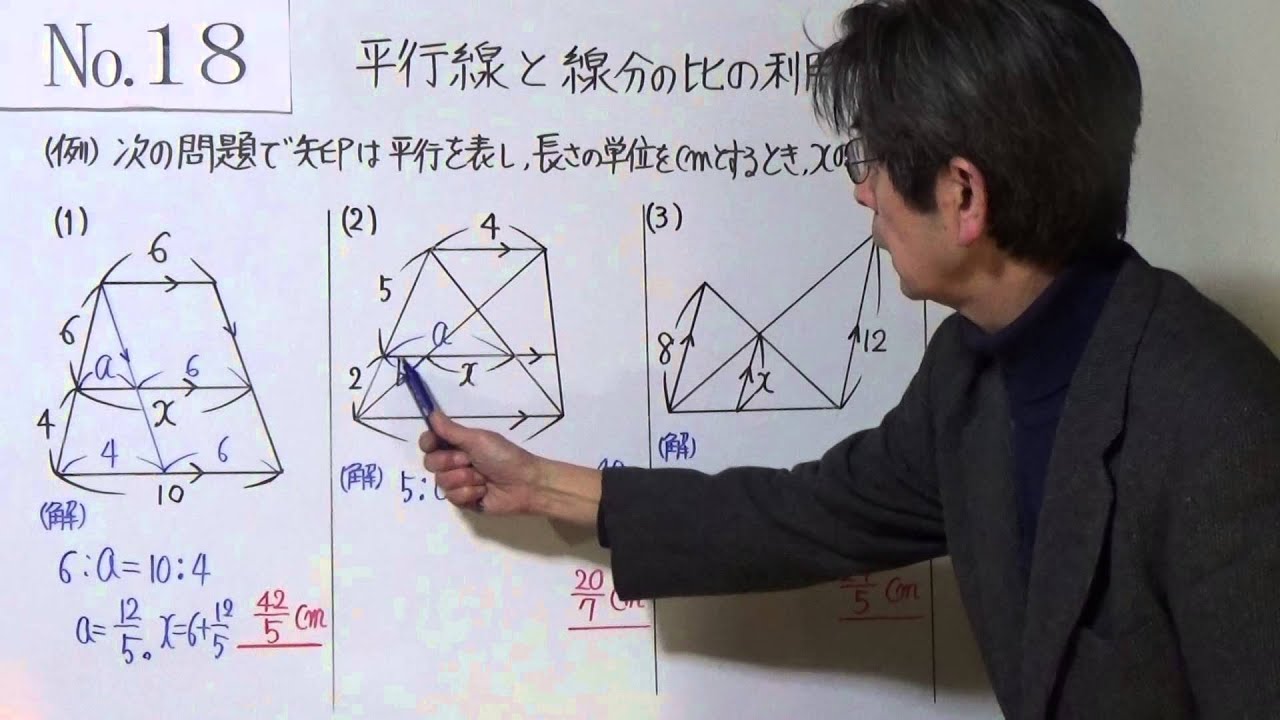
練習プリントをダウンロード https//ecommonsbiz/wpcontent/uploads//11/DB118pdf 動画リンク 中点連結定理 https//youtube/esb6CbCDlb0平行線と線分の比 上の図3のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず応用問題の(1)で比を合わせましたね。 平行線の線分比の性質を使った問題です。 図形を見てどことどこが相似になりそうかわかるようになると良いですね。



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




中3数学 平行線と比3 平行 線分比 映像授業のtry It トライイット
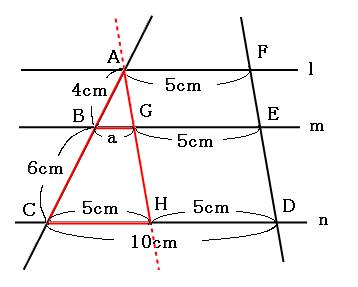
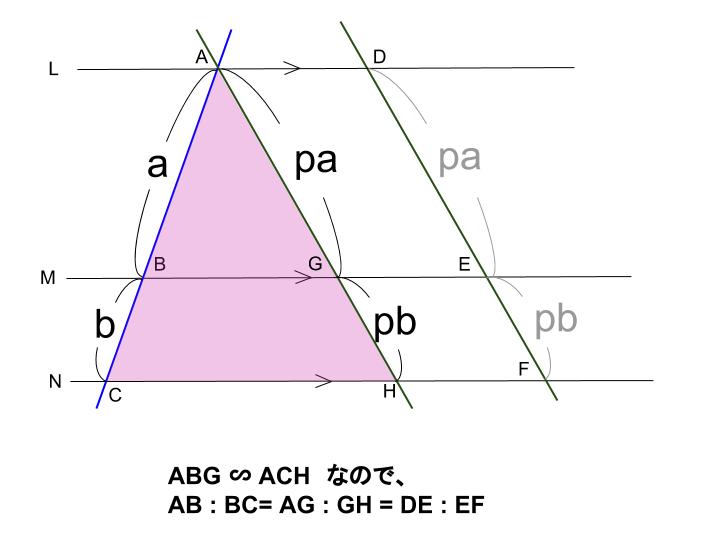
なぜ、この補助線を書いたかというと、 この補助線があると、平行と線分比の関係をうまく使えるからなんじゃ 具体的に見ていくかのぉ まず、ax xd を考えてみるかのぉ 図で考えると、ax xd というのは、以下の感じじゃ(t と t' の間の空間は平行四辺形) 実は、3本の平行線 (に交わる �中学3年生 平行線と線分の比、基本編、応用編、中点連結定理編 みなさん、初めまして。 本講座を担当している葉一(はいち)と申します。 私は元塾講師なのですが、




数学 中3 51 平行線と線分の比 中点連結定理編 Youtube




平面図形をマスター 三角形の面積比 応用編その2
問題17(3角形で平行な補助線を引く・応用2) 5回 問題18(平行四辺形で線分比・相似利用・応用1) 5回 問題19(長方形と線分比・相似比) 5回 問題(平行四辺形と合同、相似・応用2) 6回 問題21(平行四辺形で線分比・相似利用・応用3) 6回三角形の面積比~基本編~ 相似な図形 kaztastudy 相似平行線と比の利用、辺の長さを求める方法をまとめて問題解説!今回は、中3で学習する 『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な・数学中350 平行線と線分の比②(応用編) 1045 ・中3数学15④平行線と線分の比の利用(2)裏技 1404 ・中1数学方程式(時計)(1) 842 ・平行線と線分の比_05 平行線と比の発展




相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
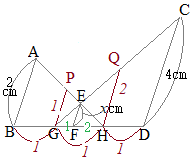



相似図形 高校入試問題
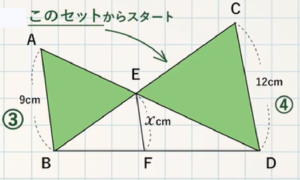
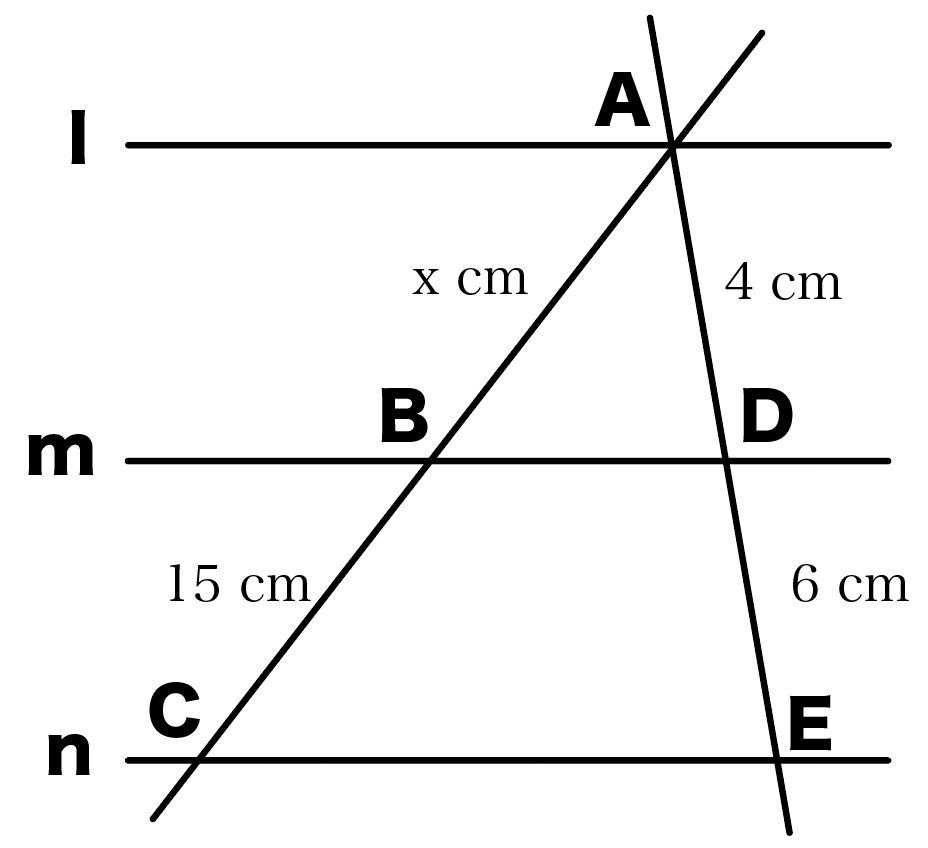
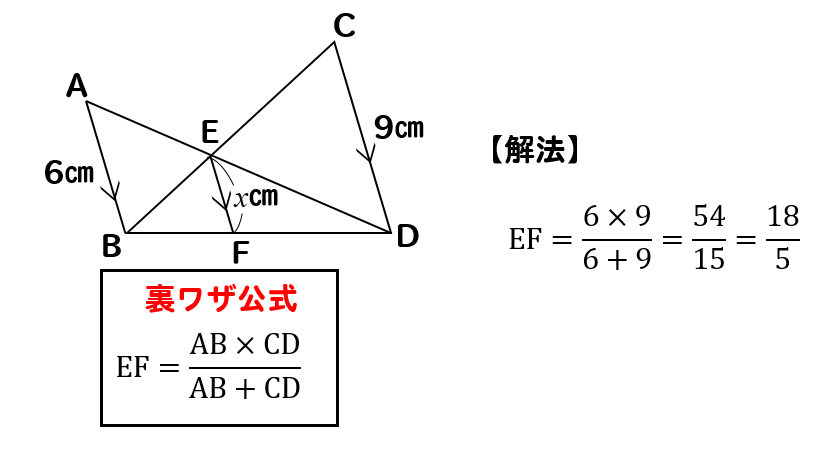
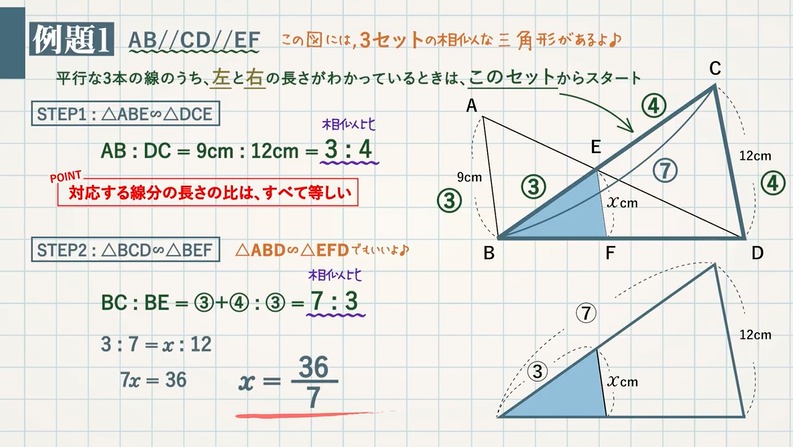
平行な $3$ 本の線のうち、左と右の長さがわかっているときは、$\rm ABE$ と $\rm DCE$ からスタート STEP $\textcolor{blue}{1}$ : $\textcolor{blue}{\rm ABE∽ DCE}$ $\rm ABDC=9cm12cm=\textcolor{blue}{34}$ (相似比) POINT:対応する線分の長さの比は、すべて等し中学3年平行線と線分 平行線と線分の比 応用 ※現在日本語と韓国・朝鮮語、中国語、ポルトガル語、ベトナム語に対応しております。 韓国・朝鮮語|中国語|ポルトガル語|ベトナム語|フィリピ訂正後中3数学講座第5章 図形と相似(7)平行線と線分比①基本 pdf 有料講座をご覧いただくにはログインが必要です。 ユーザー登録がお済みの方は、 ログイン 。



中学数学 図形の相似



平行線と線分の比についてです この図形に平行線と線分の比があるのですが Yahoo 知恵袋
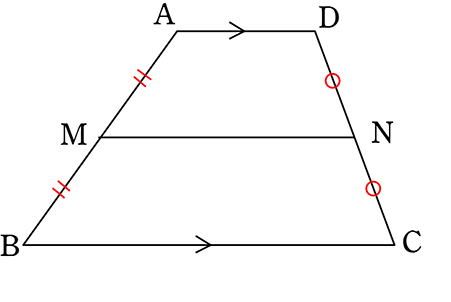
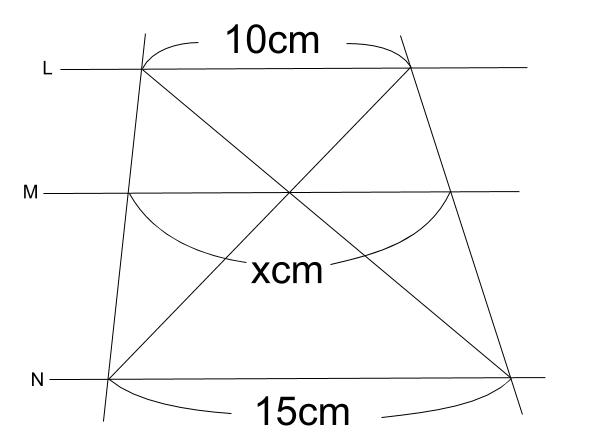
FdData 中間期末:中学数学3 年:平行線 三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内数学35章図形と相似「平行線と線分の比」<応用問題①> 組 番 名前 1右の図は,ADとBCが平行な台形ABCDです。 AD:BC=1:3とします。 辺ABの中点をM,辺CBの中点をNとし, MとNを結んだら,線分MNの長さが4㎝で した。相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似



1




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
平行線で区切られた線分の比の定理 「平行線と比の定理」の 型と 型は、台形のようなものにも応用できますね!平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\) が平行Ad:bc=1:3とします。 辺abの中点をm,辺cbの中点をnとし, mとnを結んだら,線分mnの長さが4㎝で した。 このとき,次
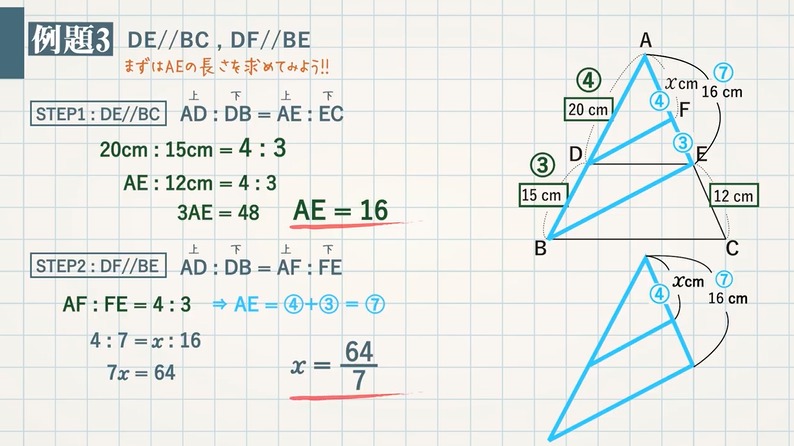



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
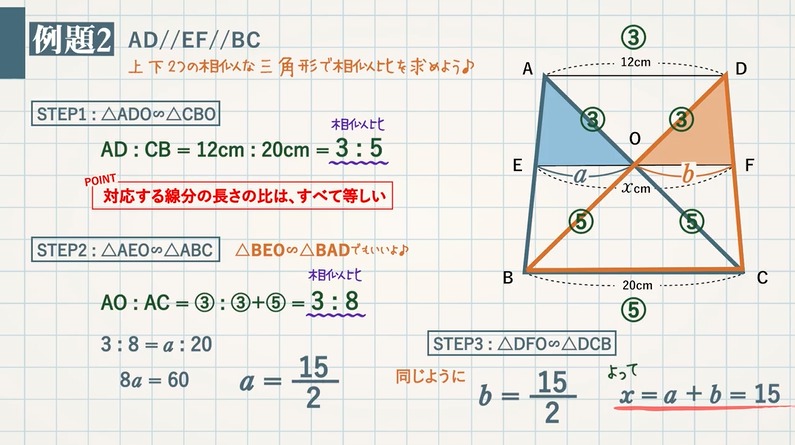



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
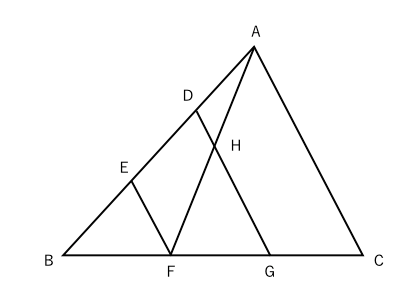
補助線で相似をつくる。 よく使う相似の形。 afの延長線とdcの延長線の交点をhとする。 するとab//cdから abf∽ hcfとなる。 bffc=21なので相似比は21である abとhcが対応する辺なので ab=4とするとhc=2となる。 また、ab//cdから aeg∽ hdgとなる。 ab=4ならcd=4なのでhd=62/5時 ・ 平行線と線分の比に関する性質を理解する。 ・ 平行線と線分の比の性質を利用して、辺の長さを求めることができる。 前時のまとめを基に、平行線と線分の比の性質について確認する。 本時の学習内容「平行線と線分の比の関係について平行線と線分_平行線と線分の比_応用(京都教育大学) 平行線と線分_平行線と線分の比_相似比等(京都教育大学) 平行線と比_中点連結定理(京都教育大学) 平行線と比_三角形と比(京都教育大学) 三角形の相似条件_二辺比夾角相等(京都教育大学




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
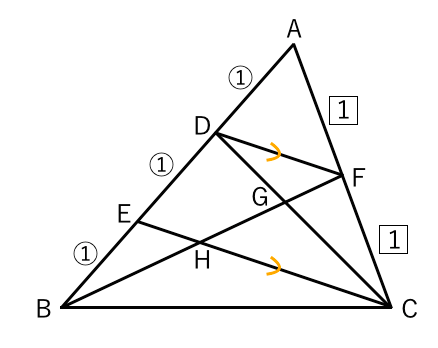
平行線と線 分の比 平行線と線 分の比に関 する性質を 見いだし,そ れを証明し, 利用するこ とができる。 三角形の1つの 辺に平行な直線 を引き、そこに できる線分の比 について長さを 調べ、それを証 明する。 平行線と線分の 比についての性質 に関心数学35章図形と相似「平行線と線分の比」<応用問題①> 組 番 名前 1右の図は,adとbcが平行な台形abcdです。 ∠bcd=∠adc=90°,∠acd=30°相似と線分比2 addb=34, eはbcの中点である。 affeを求めよ。 a b c d e f aを通り、bcに平行な直線と、cdの延長線との交点をpと
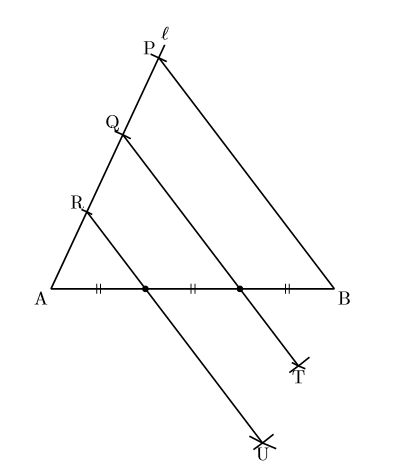



中学数学 3等分線を考える 数樂管理人のブログ




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット




Ac Be E 5cn Descubre Como Resolverlo En Qanda




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学




中学3年数学 相似の応用 線分比の移動 Youtube




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



第5章18 相似の応用 線分の比の移動 2 フロントエンドなブログ
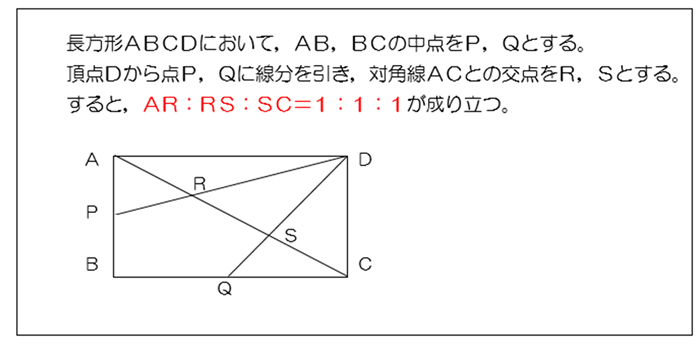



授業実践記録 数学 新しい 定理 とその活用 啓林館




世界一わかりやすい数学問題集中3 5章 図形と相似




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット



平行線と線分の比 Youtube




無料 中3数学 発展 応用問題 解答プリント 328 図形の相似3 線分の比



中3 18 5 平行線と線分の比の応用 Youtube




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



中学三年生数学図形問題 応用 あおぞら塾




数学できる人 と 数学できない人 のたった1つの違い Nghenhachay Net



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
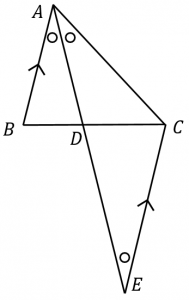



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学




中3数学 図形と相似23 平行線と線分の比 比の合成 連比 すべて無料 星組の中学数学講座




平行線と線分の比 無料で使える中学学習プリント




平行線と線分の比 辺の長さを求める応用問題4選 教遊者



1




Ac Be E 5cn Descubre Como Resolverlo En Qanda




平面図形をマスター 三角形の面積比 応用編その2
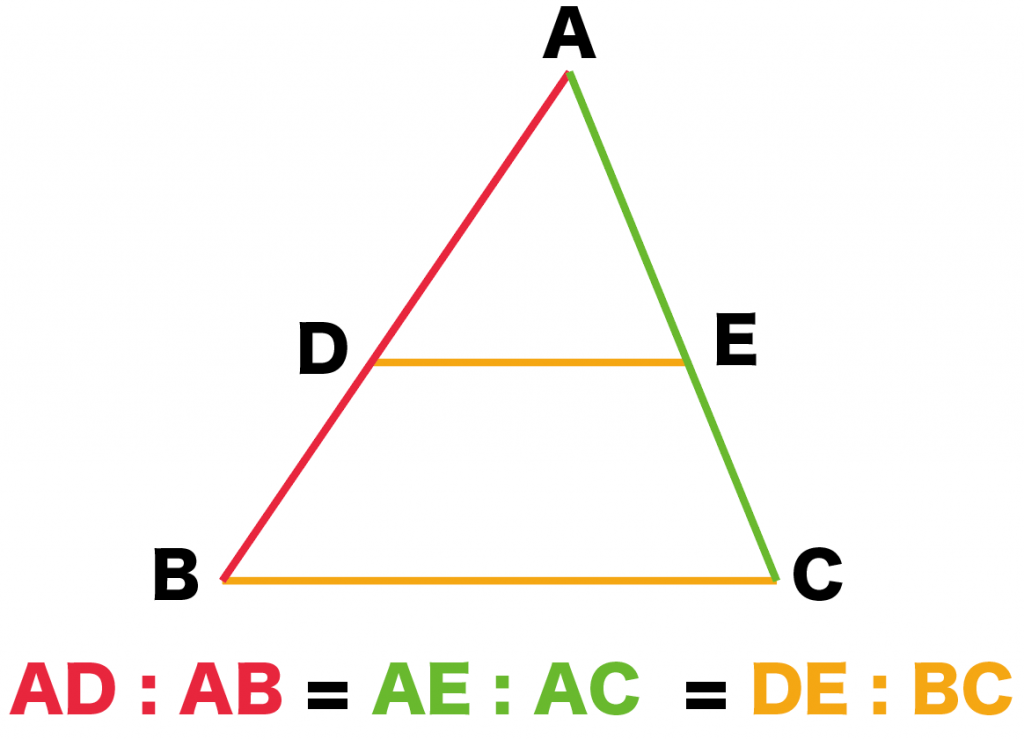



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



中3数学 中点連結定理ってどんな定理 まなビタミン



相似な図形 平行線と線分の比 よく出る系 苦手な数学を簡単に




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題




世界一わかりやすい数学問題集中3 5章 図形と相似




平面図形をマスター 三角形の面積比 応用編その2




中学3年の数学 動画 平行線と線分の比 基本編の問題 19ch




平行線と線分の比の定理 の問題の解き方 数学fun




質問です 1 の台形の問題なのですが 6 5分の12の答えが Clear



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




解き方が分かりません Ab Cd Ab Ef Bg Gh Hd Ab 2cm Clear



Q Tbn And9gcs8yek Ytk4aevkupzlfiomyr1swah7y0fxr8n2 Yhcmpzyumt Usqp Cau



中3数学平行線と線分の比の利用平行線と線分の比の利用の問題でどうしても Yahoo 知恵袋
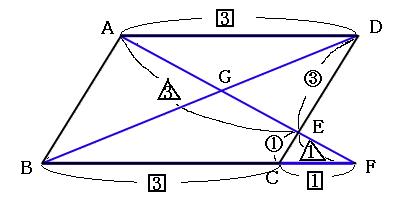



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ
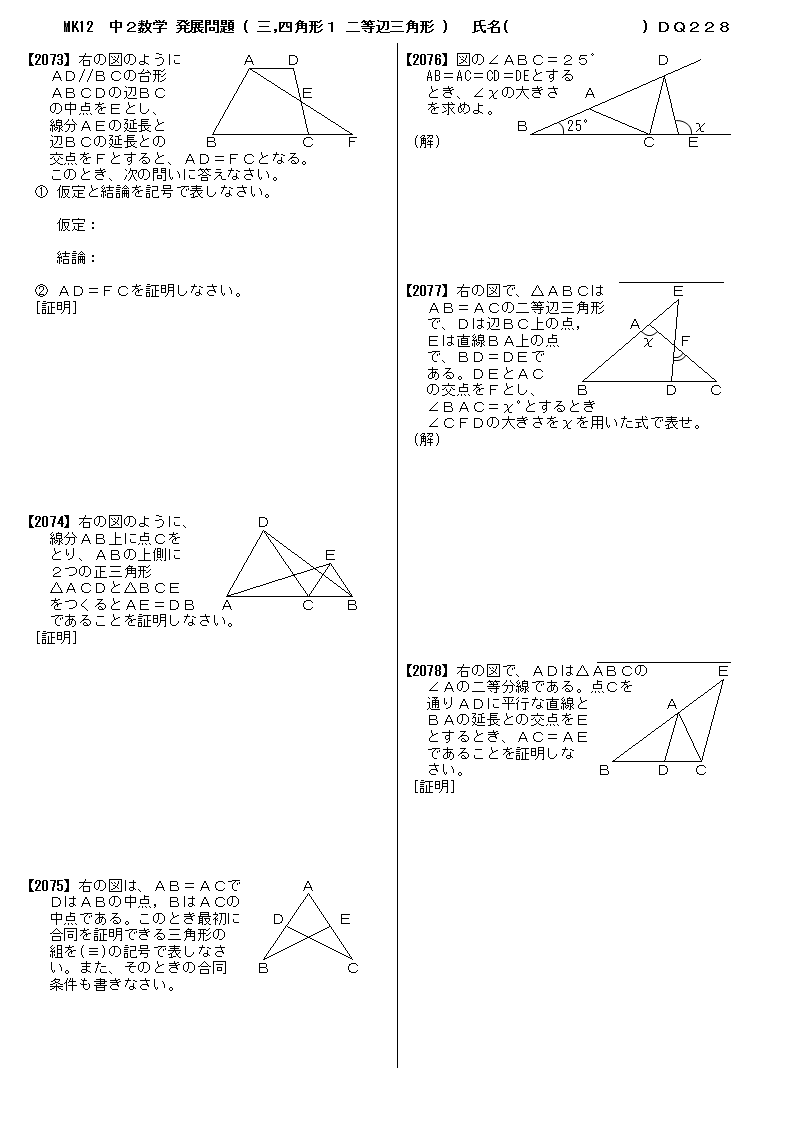



無料 中2数学 応用 発展問題 問題プリント 328 図形の相似3 線分の比




数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ



Mathematics 相似 3 平行線と比 みんなが苦手な相似頻出問題 働きアリ The 2nd




平行線と線分の比 06 平行線と比の発展問題 その2 Youtube



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典




中3数学 図形と相似21 平行線と線分の比 比の合成 連比 すべて無料 星組の中学数学講座
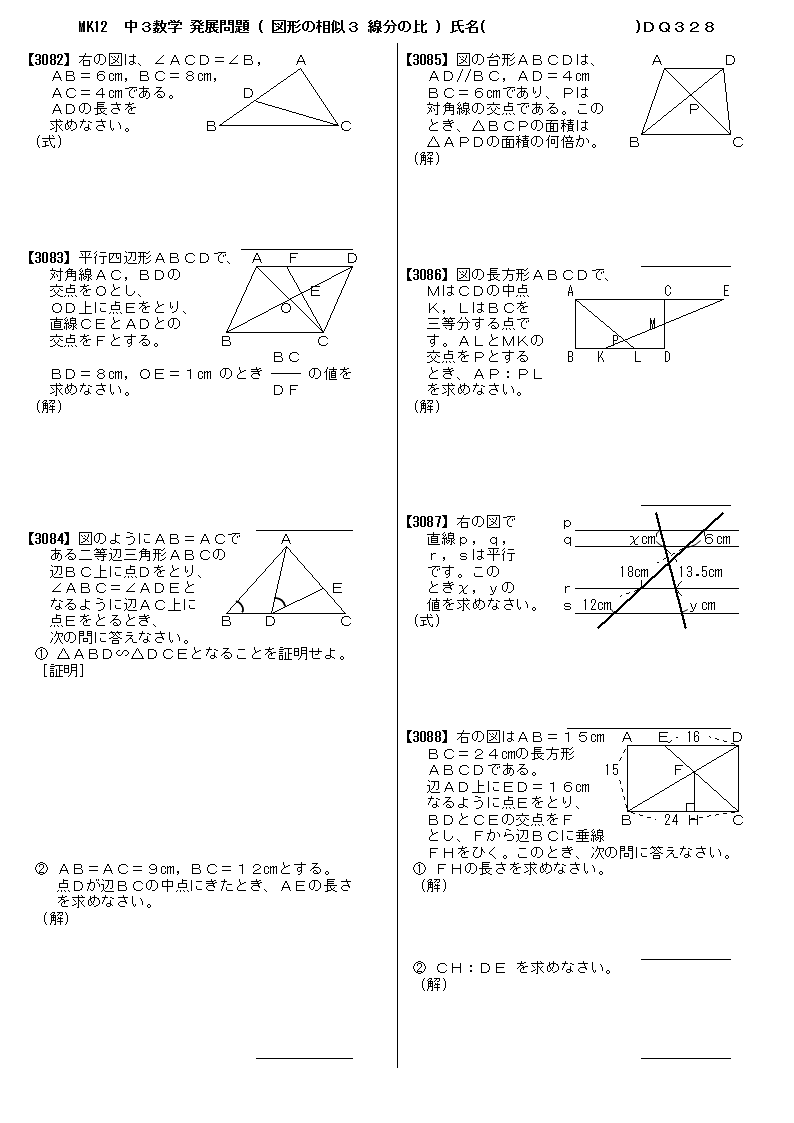



無料 中3数学 発展 応用問題 問題プリント 328 図形の相似3 線分の比
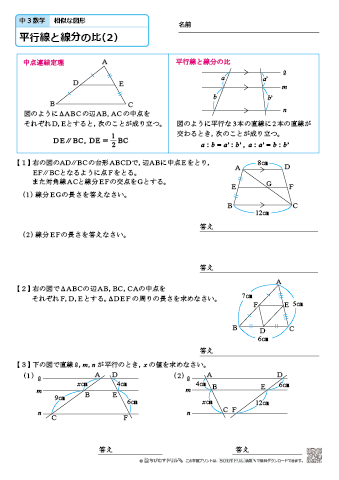



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中3 5章 図形と相似



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
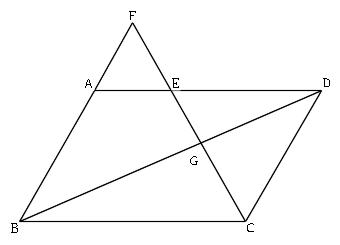



Mathematics 相似 3 平行線と比 みんなが苦手な相似頻出問題 働きアリ
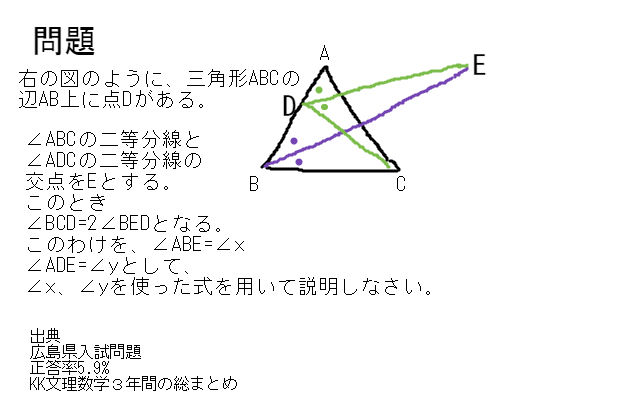



正答率5 9 の問題 平行線と角 チャレンジを 制限3分 中学数学 理科 寺子屋塾の復習サイト



面積が何倍かを求める問題 応用編 苦手な数学を簡単に




平面図形をマスター 三角形の面積比 応用編その2




数学 平行 と 線分比 の関係についてまとめました 知っておくと応用がきくよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし
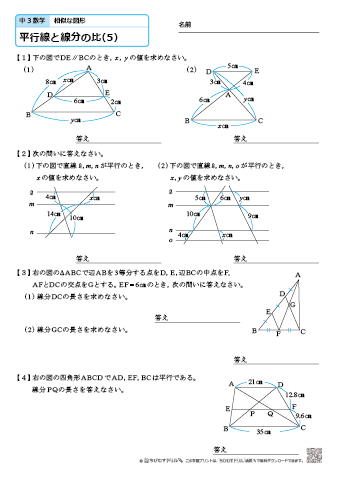



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
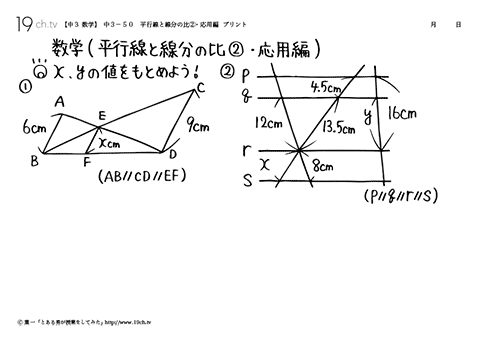



中学3年の数学 動画 平行線と線分の比 応用編の問題 19ch



相似の応用 規則集1 中学から数学だいすき




数学 中3 49 平行線と線分の比 基本編 Youtube
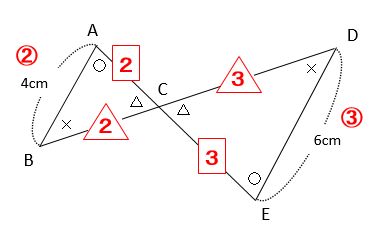



相似 平行線と三角形の問題ではちょうちょかピラミッドを探せ みみずく戦略室
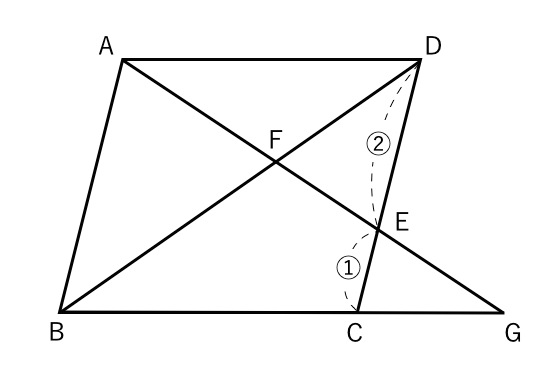



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
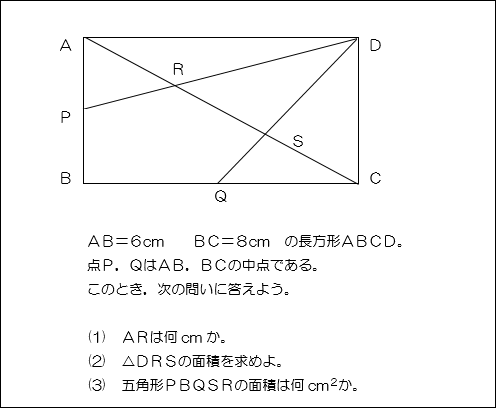



授業実践記録 数学 新しい 定理 とその活用 啓林館




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



第5章17 相似の応用 線分の比の移動 プログラミングの雫



1



これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su




三角形の合同の応用 算数 数学が好きになりmath
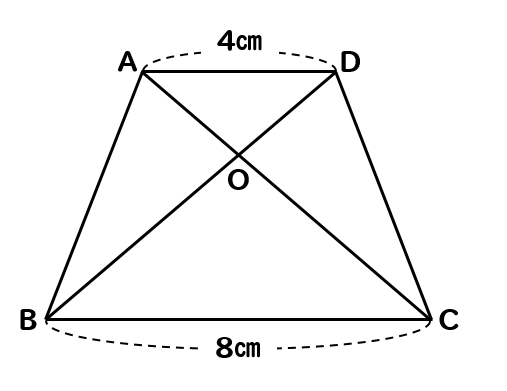



相似 台形と面積比の問題を徹底解説 数スタ




数学 平行と線分比をシッカリわかると メネラウスの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
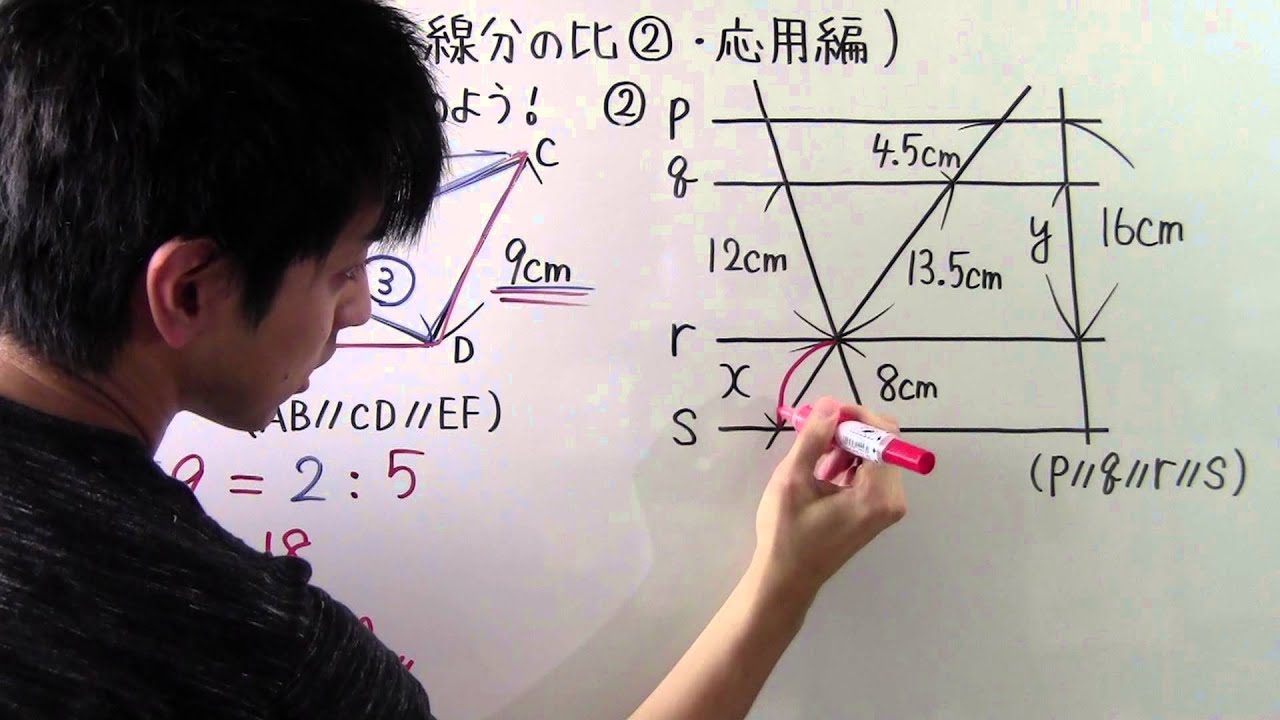



数学 中3 50 平行線と線分の比 応用編 Youtube
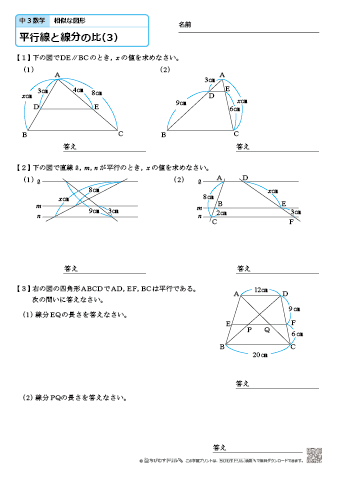



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
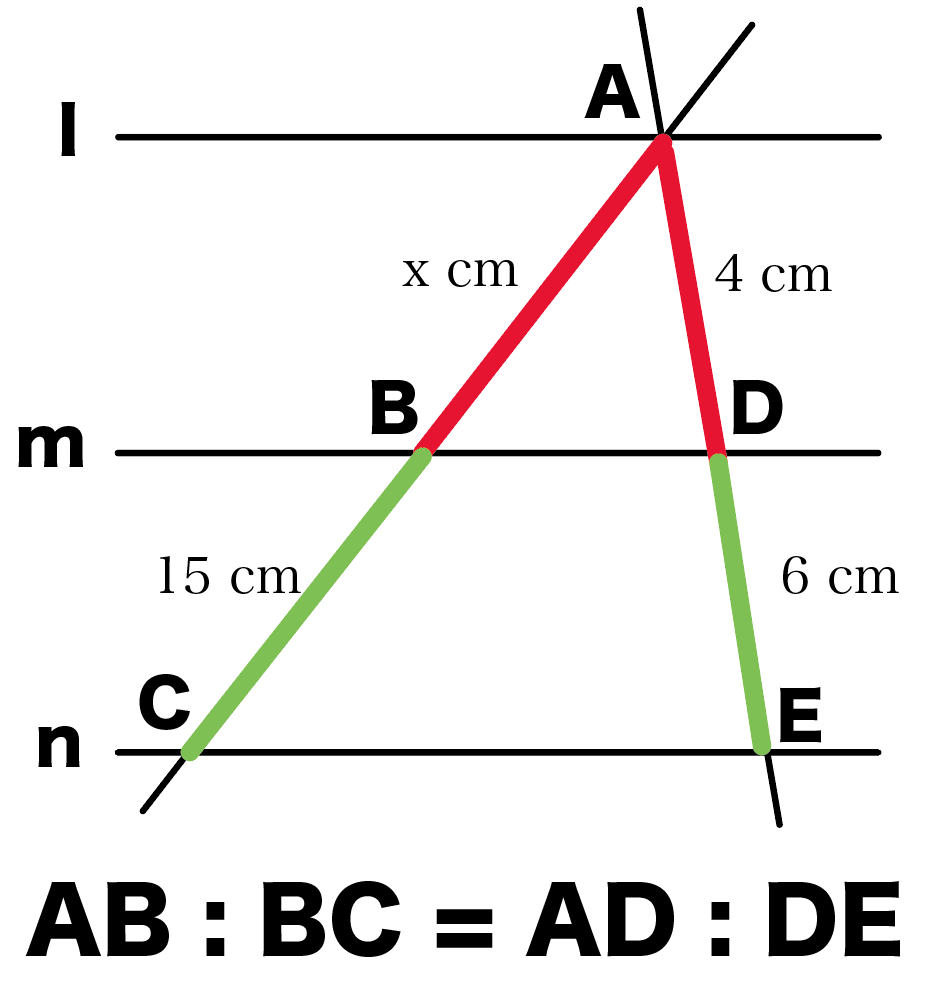



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平行線と線分の比



今日授業で平行線と線分の比に入ったのですが この応用問題がわからな Yahoo 知恵袋



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ
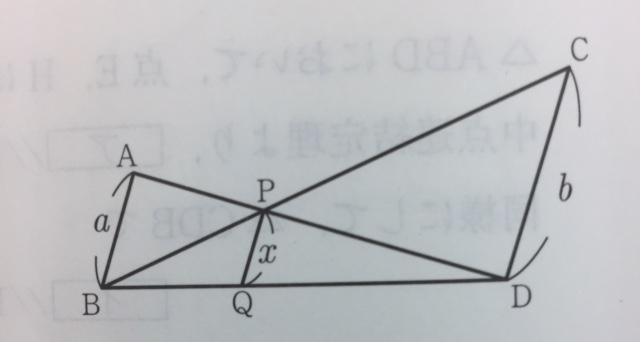



相似 平行線と線分の比 石川県金沢市の個別塾 学習塾 ナビ個別指導学院 泉が丘校ブログ



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿